NMFの乗法更新則と勾配降下法の関係

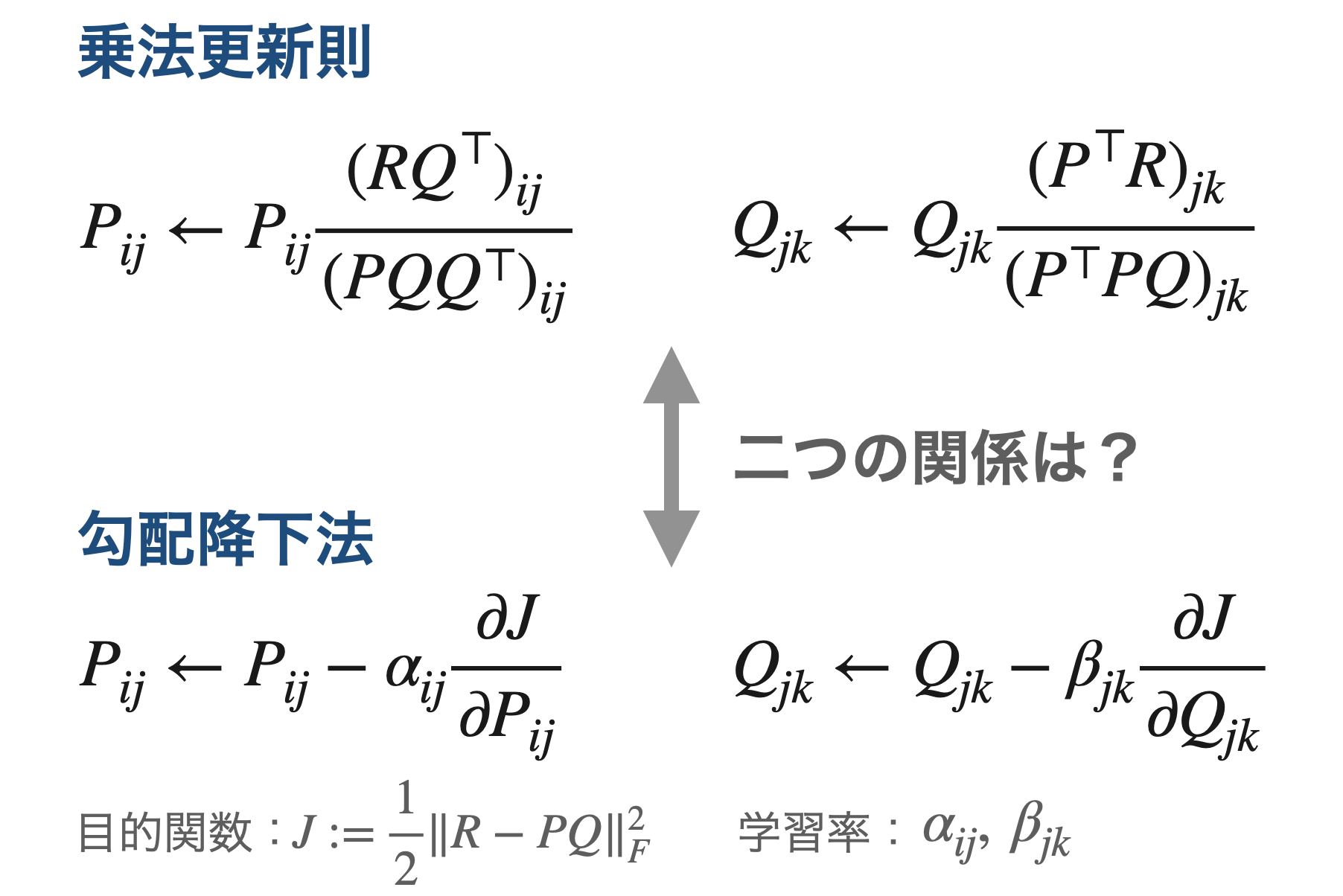
非負値行列因子分解（NMF）の乗法更新則と勾配降下法（最急降下法）にはある関係があります。

それは「乗法更新則は、得られる行列が非負という制約を必ず満たすように学習率を調整した勾配降下法である」というものです。今回はこのことを目的関数がユークリッド距離の場合に限定して、数式と数値シミュレーションで確認します。

導出に使用する公式（事前準備）

ユークリッド距離（フロベニウスノルムの二乗）の勾配を求めるためには、トレースの性質とトレースの勾配の知識が必要です。ここでは、導出に使用する各公式を載せておきました。

トレースの性質

行列$A, B$の和のトレースとそれぞれのトレースの和は等しくなります。

$$ \mathrm{tr}(A + B) = \mathrm{tr}(A) + \mathrm{tr}(B) $$

行列$A, B$の行列積$AB$のトレースとその行列の転置のトレースは等しいです。

$$ \mathrm{tr}(AB) = \mathrm{tr}(B^\top A^\top) $$

ユークリッド距離とトレースの関係

次のように、行列$A$のフロベニウスノルムの二乗はトレースを使って表現できます。

$$ \lVert A \rVert^2 _ F = \mathrm{tr}({A^\top A}) = \mathrm{tr}({A A^\top}) $$

トレースの勾配

行列$X$に関する勾配は、以下の公式が成り立ちます。

$$ \frac{\partial \mathrm{tr}(XC)}{\partial X} = C^\top $$

$$ \frac{\partial \mathrm{tr}(XCX^\top)}{\partial X} = X(C + C^\top) $$

$$ \frac{\partial \mathrm{tr}(DX)}{\partial X} = D^\top $$

$$ \frac{\partial \mathrm{tr}(X^\top D X)}{\partial X} = (D + D^\top)X $$

勾配降下法から乗法更新則の導出

非負の行列$R$を非負の行列$P, Q$に因子分解すること考えます。

このとき、$R$と$PQ$の近さをユークリッド距離で評価することにすると、最小化すべき目的関数$J$は次式で与えられます。

$$ J := \frac{1}{2}\lVert R - PQ \rVert^2 _ F $$

ここで、$P$の$i$行$j$列目の要素を$P_{ij}$、$Q$の$j$行$k$列目の要素を$Q_{jk}$とすれば、各要素への勾配降下法は次のようになります。

$$ P _ {ij} \leftarrow P _ {ij} - \alpha_{ij} \frac{\partial J}{\partial P _ {ij}} $$

$$ Q _ {jk} \leftarrow Q _ {jk} - \beta _ {jk} \frac{\partial J}{\partial Q _ {jk}} $$

ここでの、$\alpha _ {ij}(>0)$と$\beta _ {jk}(>0)$はこちらで設定する学習率であり、学習率の添字は$P$と$Q$の要素それぞれに学習率が与えられていることを意味しています。また、$\frac{\partial J}{\partial P _ {ij}}$は$J$の$P$に対する勾配の$i$行$j$列目の要素を表しており、$\frac{\partial J}{\partial Q _ {ik}}$は$J$の$Q$に対する勾配の$j$行$k$列目の要素を表しています。

続いて、具体的に勾配を導出します。準備として、$J$をトレースの形で書き直します。

$$ \begin{aligned} J &= \frac{1}{2}\mathrm{tr}((R - PQ)(R - PQ)^\top) \\ &= \frac{1}{2}\mathrm{tr}(R R^\top - P Q R^\top - R Q^\top P^\top + P Q Q^\top P^\top) \\ &= \frac{1}{2}\mathrm{tr}(R R^\top) - \mathrm{tr}(P Q R^\top) + \frac{1}{2}\mathrm{tr}(P Q Q^\top P^\top) \end{aligned} $$

この式の$P$に関する勾配を求めます。

$$ \frac{\partial J}{\partial P} = - (R Q^\top) + (P Q Q^\top) $$

勾配を$i$行$j$列目の要素である$\frac{\partial J}{\partial P _ {ij}}$だけで書き直すと次式になります。

$$ \frac{\partial J}{\partial P_{ij}} = - (R Q^\top) _ {ij} + (P Q Q^\top) _ {ij} $$

これを勾配降下法の式に代入すると次のようになります。

$$ P _ {ij} \leftarrow P _ {ij} + \alpha_{ij}((R Q^\top) _ {ij} - (P Q Q^\top) _ {ij}) $$

上式をよく見てみると、この勾配降下法のままでは更新前に$R$と$P$と$Q$は非負だとしても、$(R Q^\top) _ {ij} - (P Q Q^\top) _ {ij} < 0$の可能性があるので更新によっては$P _ {ij}$が負になり得ます。そのため、学習率をうまく設定してあげることによって、負になる原因である$-2\alpha_{ij}(P Q Q^\top)$の部分を消すことができないかを考えます。

そのような考えのもとで、学習率を以下のように与えます。 $$ \alpha _ {ij} = \frac{P _ {ij}}{(PQQ^\top)} _ {ij} $$

勾配降下法の式に学習率を代入して

$$ P _ {ij} \leftarrow P _ {ij} + \frac{P _ {ij}}{(PQQ^\top)} _ {ij}((R Q^\top) _ {ij} - (P Q Q^\top) _ {ij}) $$

整理すると次のようになります。

$$ P _ {ij} \leftarrow P _ {ij} \frac{(R Q^\top) _ {ij}}{(PQQ^\top)_ {ij}} $$

乗法更新則と同じ式を得ることができました。この式では更新前の$P$と$Q$と$R$が非負であれば更新後も非負になります（正×正=正、正+正=正、正×0=0、正+0=正、0×0=0、0+0=0であることと、内積計算は積と和からなるため）。

以上の導出過程とその結果から、乗法更新則というのは、$P$が非負になるように学習率$\alpha _ {ij}$を更新ごとに変動させて勾配降下法を適用していると解釈することができます。ちなみに、この学習率の与え方以外にも非負になり得ることからかなり保守的な更新法とも言えます。

また、$Q$についても同じような流れで勾配降下法の式から乗法更新則を導出することができます。加えて、$P$の場合と同様に、$Q$が非負になるように学習率$\beta _ {ik}$を変動させて勾配降下法を適用していると解釈することができます。

数値シミュレーション

ここでは、勾配降下法の学習率を固定した場合と乗法更新則と同じになるよう学習率を変化させた場合の学習結果の違いを確認します。

from typing import Tuple
import numpy as np


def gradient_descent_P(R: np.ndarray, P: np.ndarray, Q: np.ndarray, alpha: np.ndarray) -> Tuple[np.ndarray]:
  """ユークリッド距離によるNMFにおいて勾配降下法による更新後のPを求める
  """
  P += alpha * (R @ Q.T - P @ Q @ Q.T)
  return P

def gradient_descent_Q(R: np.ndarray, P: np.ndarray, Q: np.ndarray, beta: np.ndarray) -> Tuple[np.ndarray]:
  """ユークリッド距離によるNMFにおいて勾配降下法による更新後のQを求める
  """
  Q += beta * (P.T @ R - P.T @ P @ Q)
  return Q

まずは、学習率を全て0.01にした場合の勾配降下法を試してみます。

m, n = 3, 3
R = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])  # PとQで再構成させる対象となる行列
n_components = 2  # 圧縮次元数
maxiter = 2000  # PとQの更新回数
np.random.seed(3)
P = np.random.uniform(low=1.0E-5, high=1, size=(m, n_components))
Q = np.random.uniform(low=1.0E-5, high=1, size=(n_components, n))
for i in range(maxiter):
  P = gradient_descent_P(R, P, Q, 0.01)
  Q = gradient_descent_Q(R, P, Q, 0.01)
print(P)
print(Q)
print(P @ Q)

# P
[[-0.20295725  1.25588122]  # Pの要素に負の値が存在
 [ 1.09675161  1.92960834]
 [ 2.39646048  2.60333547]]
# Q
[[1.748946   1.36809786 0.98724972]
 [1.07889285 1.81359936 2.54830588]]
# PQ
[[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]

この勾配降下法によって、$PQ$は$R$に近づきますが、$P$の要素を見てみると負の値が混じっています。この結果では、$P$と$Q$が非負であるという制約を満たせていないことがわかります。

続いて、学習率以外同じ条件で、$P$と$Q$が必ず非負となるような学習率を更新ごとに与えます。

np.random.seed(3)  # P, Qを同条件で初期化
P = np.random.uniform(low=1.0E-5, high=1, size=(m, n_components))
Q = np.random.uniform(low=1.0E-5, high=1, size=(n_components, n))
for i in range(maxiter):
  P_denominator = P @ Q @ Q.T
  P_denominator[P_denominator == 0] = 1.0E-7  # 0除算対策
  alpha = P / P_denominator
  P = gradient_descent_P(R, P, Q, alpha)

  Q_denominator = P.T @ P @ Q
  Q_denominator[Q_denominator == 0] = 1.0E-7  # 0除算対策
  beta = Q / Q_denominator
  Q = gradient_descent_Q(R, P, Q, beta)
print(P)
print(Q)
print(P @ Q)

# P
[[ 2.5307252   5.34209982]
 [11.15208646 10.11497131]
 [19.77344772 14.8878428 ]]
# Q
[[0.33120385 0.19073168 0.05025952]
 [0.03029035 0.28402886 0.53776737]]
# PQ
[[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]

この条件では、学習によって得られた行列$P$と$Q$は非負という制約を満たせていました。

まとめ

勾配降下法から非負値行列因子分解（NMF）の乗法更新則を導出することで、乗法更新則は分解後の因子行列が非負という制約をうまく満たすように学習率を調整した勾配降下法であるという関係を確認できました。

ちなみに、この記事では目的関数がユークリッド距離の場合のみを扱いましたが、参考文献の論文にはKLダイバージェンスの場合も載っているのでよかったらご覧ください。

参考文献

D. Lee and H. Seung, “Algorithms for non-negative matrix factorization,” Adv. Neural Inf. Process. Syst., no. 1, pp. 556–562, 2001.
行列ノルム - Wikipedia
跡 (線型代数学) - Wikipedia
Matrix calculus - Wikipedia

See also

• 欠損値ありデータへの協調フィルタリングには素のNMFではなく欠損値用NMFを使おう