例えば、ユーザが映画を評価できるようなWebサイトがあったとします。このとき、ユーザは全映画を評価しているかと言えばそんなことはなく、ごく一部の映画しか評価していません。つまり、大部分の映画評価データが欠損していることになります。このような欠損値のあるデータに対して、もし仮に素の非負値行列因子分解(NMF)を用いた協調フィルタリングを試そうと考えた場合、欠損値を別の値($0$や平均値など)で埋めてから実行することになります。この埋め方で何か変わるのでしょうか?この記事ではまず、埋め方によって学習結果にどのような影響があるのかを調査します。その後、欠損値を埋めないでNMFが行える手法の1つである重み付き非負値行列因子分解(WNMF)を紹介します。
非負値行列因子分解(NMF)
NMFは与えられた行列$R$に対して、$R \approx PQ$ となる非負値因子行列$P, Q$を探す問題です。
例えば、$R$と$PQ$の近さをユークリッド距離(フロベニウスノルムの二乗)で表すと
$$ \lVert R - PQ \rVert^2 _ F = \sum _ {i=1}^{m}\sum _ {j=1}^{n}(R _ {ij} - (PQ) _ {ij})^2 $$
となります。ここでお話しするNMFでは上のユークリッド距離を最小化するような正の行列$P, Q$を得るように学習します。ちなみに、添字$ij$は行列の$i$行$j$列目の要素であることを表しています。
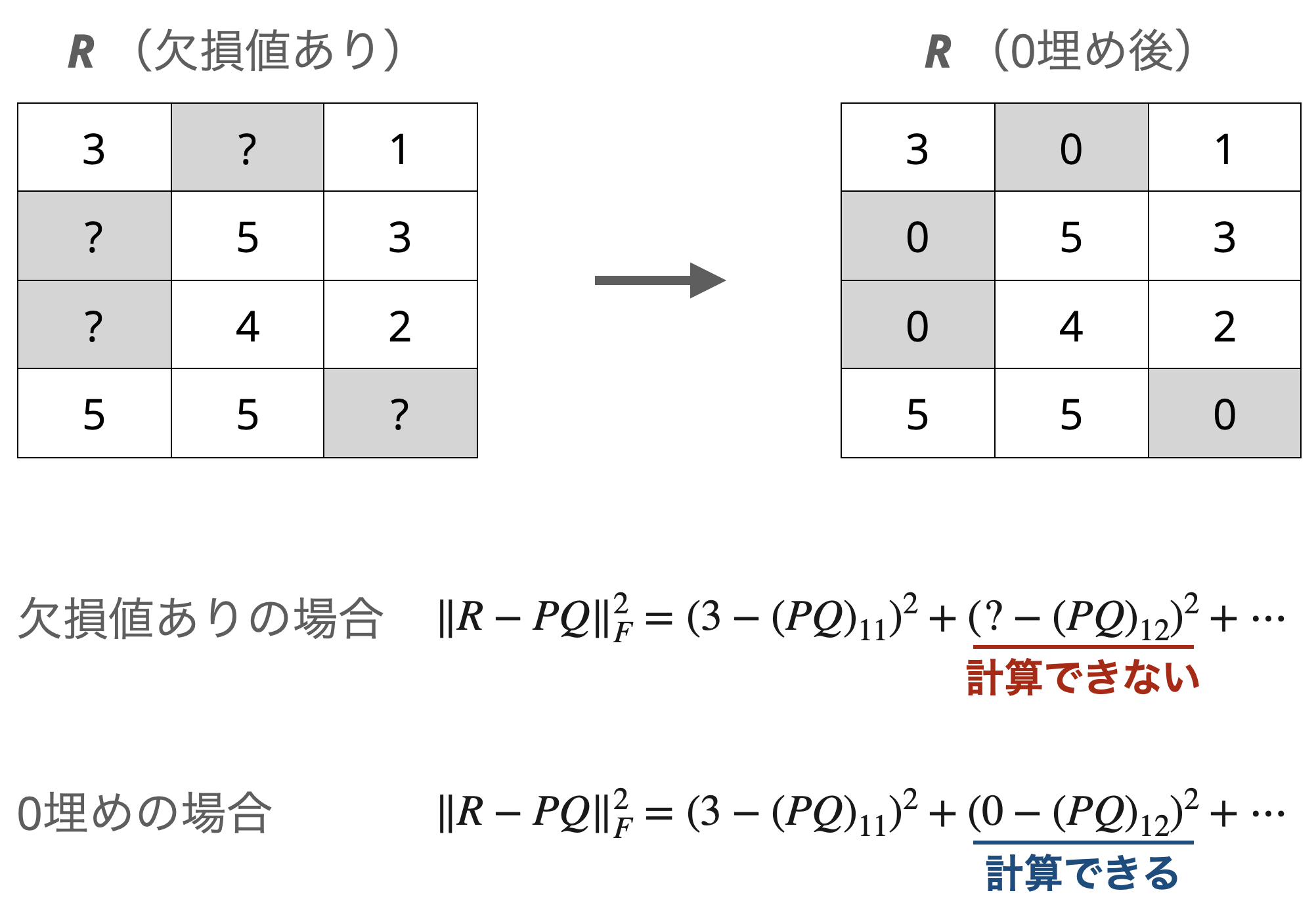
ここで、もし$R$の要素に欠損値がある場合は、ユークリッド距離の計算ができないために、何らからの具体的な値で欠損値を埋める必要があります。一番単純な方法として、$0$で埋めるというのがあります。
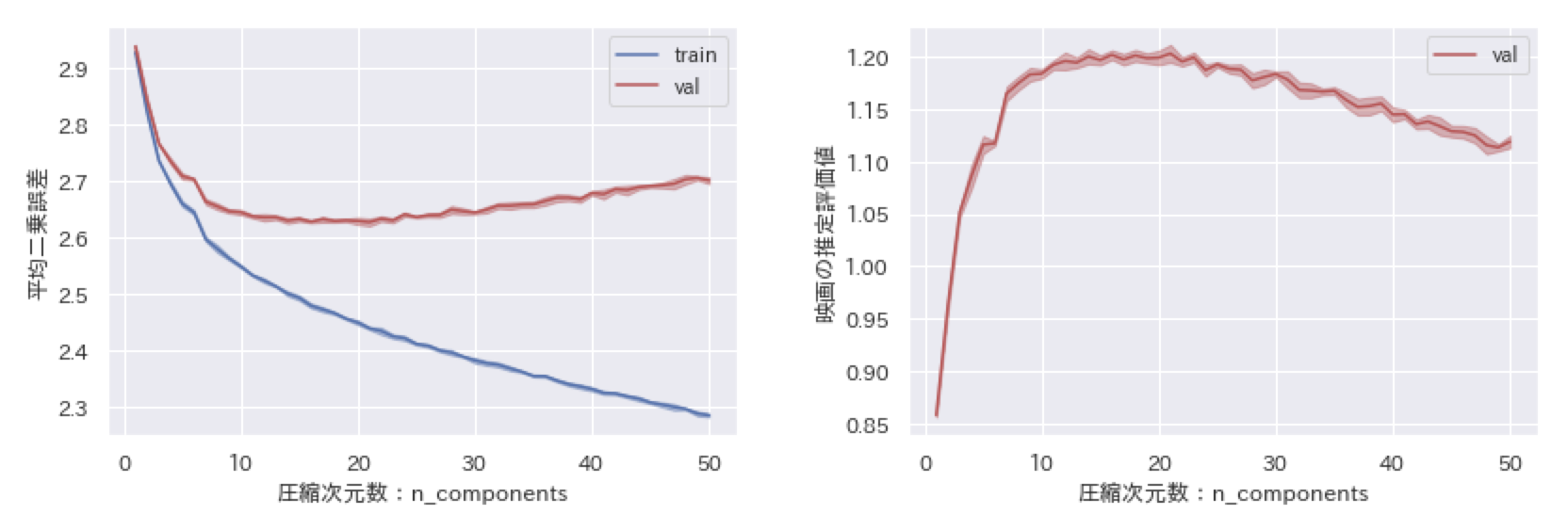
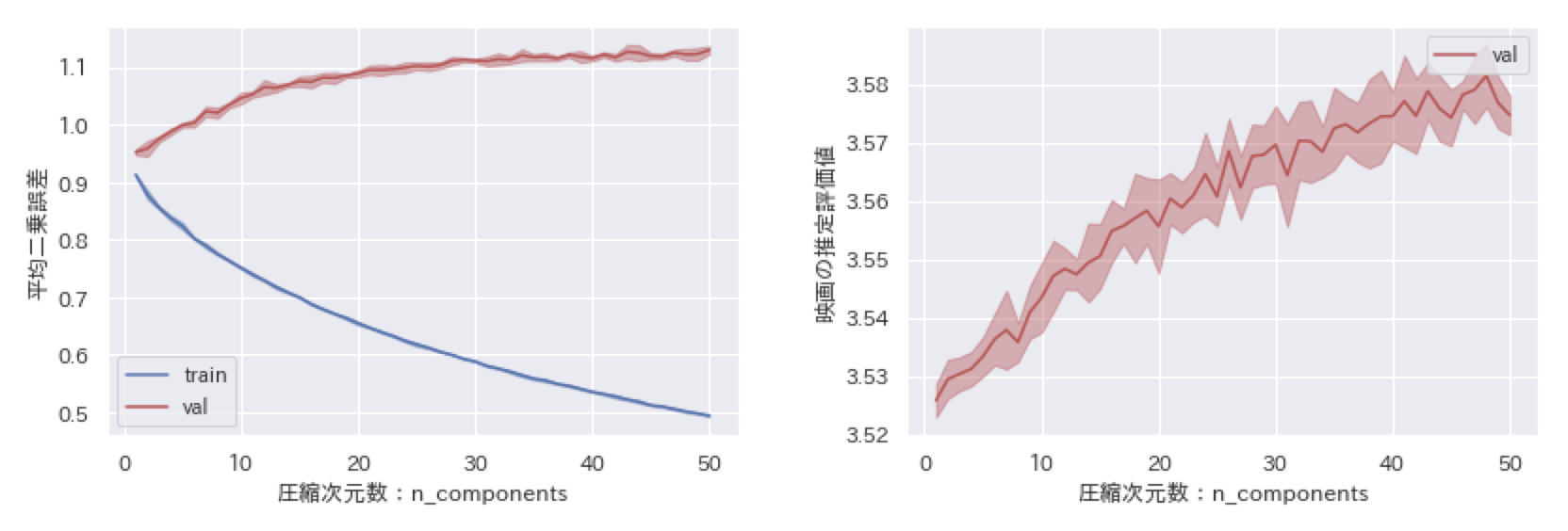
しかしながら、欠損値を$0$で埋めたことで欠損箇所に対応する$PQ$の要素が$0$に引っ張られてしまいます。このことを確かめるために、MovieLensと呼ばれる映画評価データセット(MovieLens 100K Dataset)を使って検証してみました。学習では層化$k$分割交差検証($k=5$)で訓練用データと評価用データに分けて、平均二乗誤差で評価しました(下の左図)。また、予測結果が評価データから$0$に引っ張られていることを確認するために、予測結果の平均値を載せました(下の右図)。
学習データによる結果(train)が青、評価データによる結果(val)が赤となっています。少しわかりにくいのですが、線自体は層化$k$分割交差検証($k=5$)によって5分割されたデータから得られた結果の平均値であり、線の色より薄い部分は平均値からのずれを表しています。
まず、右図を見てみると、予測評価値の平均値はどちらかと言えば$0$に近い値を取っています。評価用データの真の平均評価値を確認してみると$3.5$付近でしたので、大幅にずれていると言えます。これは欠損していてわからないというだけで本来$0$ではない値を$0$とみなして学習しているからです。ちなみに$0$は映画評価値の範囲$1$から$5$内に存在しない値です。同様の理由で、左図の平均二乗誤差が全体的に大きな値となっています。
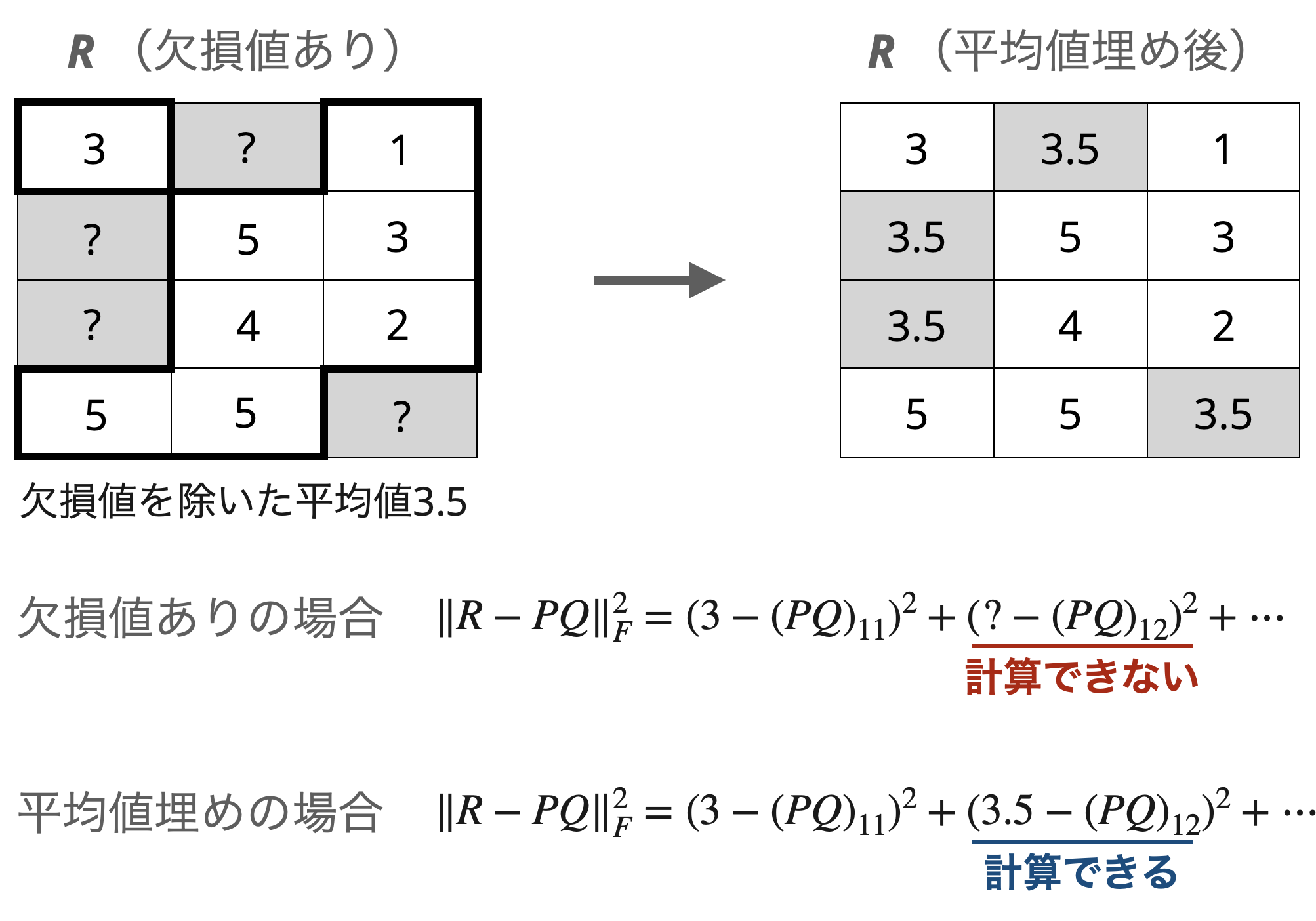
他にも統計量で埋める方法があります。例えば、平均値です。
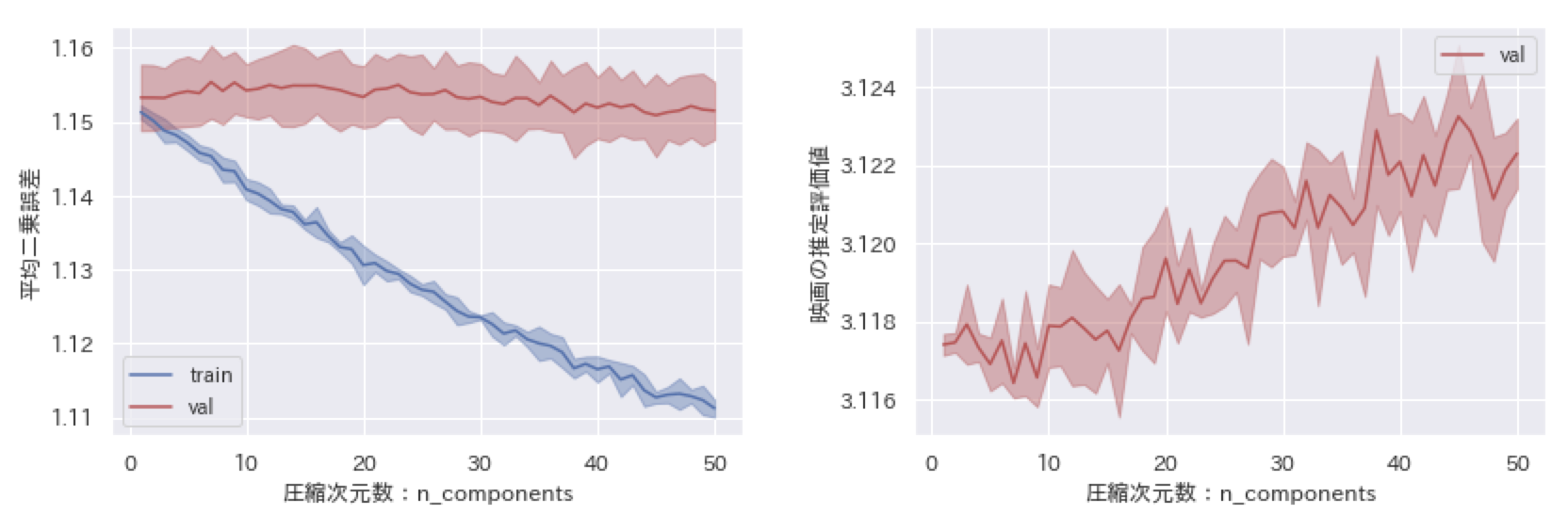
平均値で埋める以外は同条件で学習させた結果を下に図示しました。
こちらであれば評価値として存在しない$0$の場合に比べて$1$から$5$の範囲に収まるので平均二乗誤差は小さくなっています。これらの結果から、どの値で埋めるかがとても重要であり、埋めた値によっては$0$埋めのように真逆の予測結果に引っ張られてしまう可能性があります。また、平均値埋めについてもこの埋め方で問題ないかをさらに検討する必要があります。
このような欠損値の埋め方によって大きく結果が変わってしまうような方法ではなくて、欠損値のままNMFを実行することができないのでしょうか?
重み付き非負値行列因子分解(WNMF)
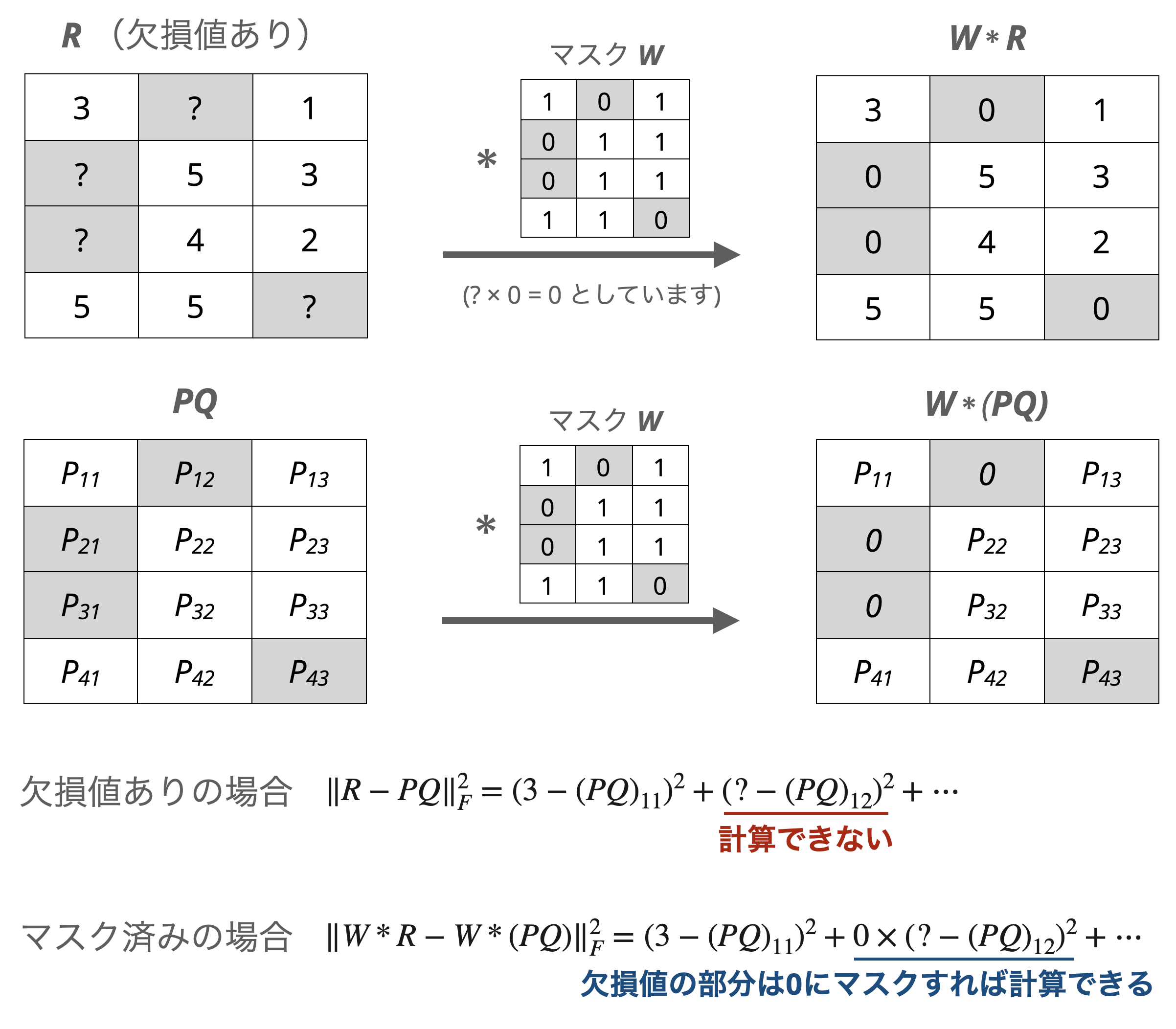
欠損値を埋めないでNMFが行える手法の1つとして、重み付き非負値行列因子分解(WNMF)が提案されています(Zhangら、2006)。この手法では$R$の欠損箇所と欠損箇所に対応する$PQ$の部分を$0$でマスクして最小化問題を考えることで、欠損値を埋めずにNMFの実行を可能にしています。
具体的には、欠損値の箇所を$0$、それ以外を$0$とする重み行列$W$としたとき、$W$によってマスクされた$R$と$PQ$を用いて近さが評価されます。
$$ \lVert W * R - W * (PQ) \rVert^2 _ F = \sum _ {i=1}^{m}\sum _ {j=1}^{n}W_{ij} * (R _ {ij} - (PQ) _ {ij})^2 $$
ここでの$*$は2つの行列の各要素同士を掛けるアダマール積を表しています。この$0$と$1$の重みを使ったマスク処理によって、欠損しているために計算できなかったユークリッド距離の計算ができるようになっています。
続いて、欠損値埋めしたNMFの場合と同条件でこのWNMFを学習させてみます。結果は次のようになりました。
左図の平均二乗誤差については平均値で埋めた場合よりも少しだけ良い結果が得られています。また、右図の推定評価値の平均値については、評価用データの真の平均評価値が$3.5$付近であったことから平均値で埋めた場合($3.1$付近)よりもよく表現できています。
まとめと今後の方向性
今回はまず、素の非負値行列因子分解(NMF)で協調フィルタリングを試しました。素のNMFの場合は欠損値を埋める必要があり、その結果埋めた値に結果が引っ張られてしまうことを確認しました。特にMovieLensのような欠損値が多いデータに対しては巣のNMFが向いていないと言えそうです。
このような問題点から欠損値が多いデータ向けに、欠損したまま非負値行列因子分解する手法がいくつか提案されており、この記事ではそのうちの1つである重み付き非負値行列因子分解(WNMF)を紹介しました。
このWNMFと呼ばれる手法は欠損箇所に対応する部分をマスキングする処理によって、欠損値のまま非負値行列因子分解が可能です。
欠損値を別の値に埋める処理が必要ないので、素のNMFで見られた推定行列$PQ$が埋めた値に引っ張られるということもありません。また、WNMFの結果は$0$埋めや平均値埋めしたNMFよりも平均二乗誤差が小さくなることと、推定評価値の平均値が真の平均値により近くなることを確認しました。
以上のことから、協調フィルタリングには素のNMFよりWNMFのような推薦用のものを使うほうが良さそうです。
ただ、今回使った評価指標は平均二乗誤差のみであり、推薦する上では素のNMFでも問題ないという結果になる可能性もあります。なので、推薦向けの評価指標を増やして適宜追記していこうと考えています。
参考文献
S. Zhang, W. Wang, J. Ford, and F. Makedon, “Learning from Incomplete Ratings Using Non-Negative Matrix Factorization,” in Proc. SIAM Int. Conf. Data Mining, pp. 549-553, 2006.
使用したコード
MovieLensデータセットの読み込み
import polars as pl
df = pl.read_csv("/content/ml-100k/u.data", sep="\t", has_header=False)
df.columns = ["user id", "item id", "rating", "timestamp"]
df_ranking = df.pivot(values="rating", index="user id", columns="item id").fill_null(0)
ranking_matrix = df_ranking[:, 1:].to_numpy() # Rに対応
層化k分割交差検証
import numpy as np
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import mean_squared_error
from scipy.sparse import csr_matrix
from tqdm import tqdm
# ユーザの割合をなるべく均一に分けたいので、層化k分割交差検証を使う
user_ids = df_ranking["user id"].to_numpy()
row_idx, col_idx = ranking_matrix.nonzero()
user_labels = [user_ids[idx] for idx in row_idx] # 基準となるユーザIDを抽出
n_iteration = 50 # NMFを実行することになる最大圧縮次元数-1
n_splits = 5 # 層化k分割交差検証での分割数
train_losses = np.zeros((n_iteration, n_splits))
val_losses = np.zeros((n_iteration, n_splits))
val_means = np.zeros((n_iteration, n_splits))
skf = StratifiedKFold(n_splits=n_splits, random_state=3, shuffle=True)
for i in tqdm(range(n_iteration)):
train_loss = [None] * n_splits
val_loss = [None] * n_splits
val_mean = [None] * n_splits
np.random.seed(3)
for j, (train_index, test_index) in enumerate(skf.split(row_idx, user_labels)):
train_ranking_matrix = np.zeros_like(ranking_matrix) # 0埋めとWNMF用なので平均埋めの場合はこちらをコメント化する
# train_ranking_matrix = np.full_like(ranking_matrix, ranking_matrix[row_idx[train_index], col_idx[train_index]].mean()) # 平均埋めの場合はこちらをコメントアウト
train_ranking_matrix[row_idx[train_index], col_idx[train_index]] = ranking_matrix[row_idx[train_index], col_idx[train_index]]
nmf = NMF(n_components=(i + 1)) # WNMFを使う場合はNMFをWNMFに置き換える
P, Q = nmf(train_ranking_matrix)
ranking_matrix_reconstruction = P @ Q
train_pred = ranking_matrix_reconstruction[row_idx[train_index], col_idx[train_index]]
val_pred = ranking_matrix_reconstruction[row_idx[test_index], col_idx[test_index]]
train_true = ranking_matrix[row_idx[train_index], col_idx[train_index]]
val_true = ranking_matrix[row_idx[test_index], col_idx[test_index]]
train_loss[j] = mean_squared_error(train_true, train_pred, squared=False)
val_loss[j] = mean_squared_error(val_true, val_pred, squared=False)
val_mean[j] = val_pred.mean()
train_losses[i] = np.asarray(train_loss)
val_losses[i] = np.asarray(val_loss)
val_means[i] = np.asarray(val_mean)
NMFとWNMFの定義
from typing import Tuple
import numpy as np
class NMF:
def __init__(self, n_components: int = 100, maxiter: int = 100, **kwargs):
self.n_components = n_components # 圧縮次元数
self.maxiter = maxiter # 最大更新数
def __call__(self, R: np.ndarray) -> Tuple[np.ndarray]:
m, n = R.shape
P = np.random.uniform(low=0, high=1, size=(m, self.n_components))
Q = np.random.uniform(low=0, high=1, size=(self.n_components, n))
for i in range(self.maxiter):
P, Q = self.multiplicative_update_rule(R, P, Q)
return P, Q
def multiplicative_update_rule(self, R: np.ndarray, P: np.ndarray, Q: np.ndarray) -> Tuple[np.ndarray]:
"""ユークリッド距離によるNMFにおいて乗法更新則による更新後のPとQを求める
"""
P_denominator = P @ Q @ Q.T # Rに対するmaskは変わらないので除いてある
P_denominator[P_denominator == 0] = 1.0E-7 # 0除算対策
P = P * (R @ Q.T) / P_denominator
Q_denominator = P.T @ P @ Q
Q_denominator[Q_denominator == 0] = 1.0E-7
Q = Q * (P.T @ R) / Q_denominator
return P, Q
class WNMF(NMF):
def __init__(self, n_components: int = 100, maxiter: int = 100, **kwargs):
super().__init__(n_components=n_components, maxiter=maxiter, **kwargs)
def multiplicative_update_rule(self, R: np.ndarray, P: np.ndarray, Q: np.ndarray) -> Tuple[np.ndarray]:
"""ユークリッド距離によるWNMFにおいて乗法更新則による更新後のPとQを求める
Rは欠損値を既に0で埋めていることを想定している
"""
P_denominator = P @ Q @ Q.T
P_denominator[P_denominator == 0] = 1.0E-7 # 0除算対策
P = P * (R @ Q.T) / P_denominator
Q_denominator = P.T @ P @ Q
Q_denominator[Q_denominator == 0] = 1.0E-7
Q = Q * (P.T @ R) / Q_denominator
return P, Q